参考文献

（本サイトの全ての図の著作権は著者に属します。）

ここの主題は「相対論」的な渦の散乱ですので、ここでは相対論的効果を観察することにします。

アインシュタインの相対性理論によれば、真空中を伝わる光速はどのような観察者から観測てしても常に一定であり、また物質は光速より速く動くことが出来ないということになります。

先ほどまでの散乱では、はじめ渦と反渦が静止している状態から初めて、渦と反渦間の引力により衝突が起こる様を見てきました。

そこで、相対論的効果を観察するために渦と反渦に初速度を与えて勢い良く衝突させてみましょう。一体どんなことが起こるでしょうか？

渦と反渦をそれぞれ光速の９０％の初速度を与えて衝突する様を以下に紹介します。ちなみに相対論的効果により光速に近い速さで動く物体は動いている方向に縮みます。これはローレンツ収縮と呼ばれる現象で、相対性理論の著しい特徴です。

初速度０での衝突との違いは明らかですね。

あまりに勢い良く衝突したため渦と反渦が対消滅する前に通り抜けてしまい、渦と反渦がオーバーシュートして透過してしまっています。このように速度にある閾値があって、その速度よりも小さければ渦と反渦は消滅してしまいますが、その速度よりも大きければ消滅せずに生き残ることが出来るというわけです。ただし、結局、渦と反渦の引力で減速していき、再び衝突が起こります。このことを何度か繰り返すと最終的には渦と反渦は消えてなくなることが予想出来ますね。

つづく

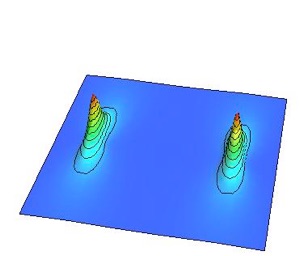
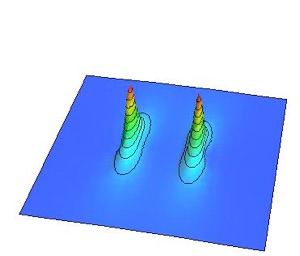
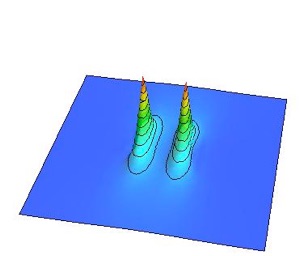
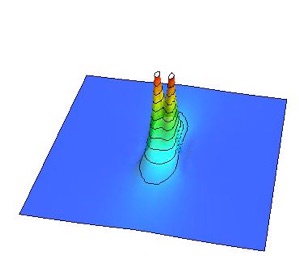
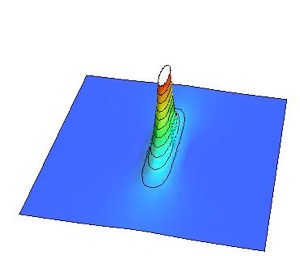
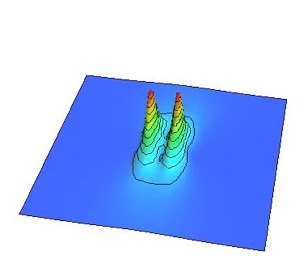
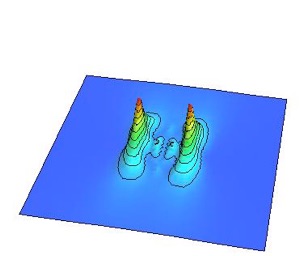
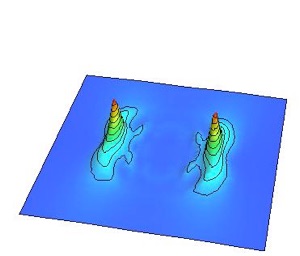
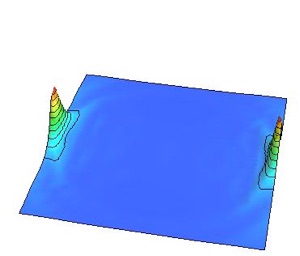
ローレンツ収縮した渦

ローレンツ収縮した反渦

光速の９０％で衝突